cs224n lecture 8 note: recurrent neural network

Published: December 23, 2018 by Learner | Hits:

• Categories:
• cs224n 8

• Tags:
• notes 8

1. 前言

这节课介绍了RNN和语言模型，引出了RNN训练中的问题，最后介绍了模型的实际应用。

2. 语言模型

语言模型就是计算一个单词序列的概率的模型。人类语言本质上是序列信号，如何处理语言的序列信息，是机器翻译、命名实体识别等众多相关领域的关键。

传统模型

传统的模型为了简化问题，引入了马尔科夫假设，一个错误但又很有必要的假设。句子的的概率通常是通过待遇测单词之前长度为n的窗口建立条件概率来预测(n-gram)：

$$P(w_1,w_2,\cdots,w_m) = \prod_{i=1}^{i=m} P(w_{i} | w_1, \cdots, w_{i-1}) \approx \prod_{i=1}^{i=m} P(w_{i} | w_{i-n}, …, w_{i-1})$$

为了估计此条件概率，常用基于计数的方法，如BiGram和TriGram，有：

$$\begin{align} P(w_2 | w_1) &= \frac {count(w_1,w_2)}{count(w_1)} \\ P(w_3 | w_1, w_2) &= \frac {count(w_1,w_2,w_3)}{count(w_1, w_2)} \end{align}$$

理论上，n-gram中的n越大，模型效果越好。不过，n很大时，继续增大n，效果增长的比例会比较小。实际中，数据量比较大而内存有限，通常采取一些平滑措施，如n取尽可能可操作的值。

RNN

新的语言模型是利用RNN对序列建模，复用不同时刻的线性非线性单元及权值，理论上之前所有的单词都会影响到预测单词。

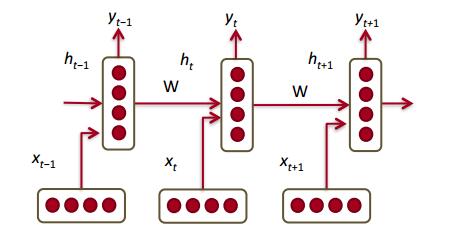
可以看到所需内存只与词表大小成正比，不取决于序列长度。

损失函数

在语言模型中，损失即为分类问题常见的交叉熵损失函数。如果以2为底数会得到“困惑度”，代表模型下结论时的困惑程度，越小越好：

$$Perplexity = 2^J$$

3. RNN的训练

RNN的一个很明显的问题就是长距离依赖问题。因为在前向传播的时候，前面的值要反复乘上W，且要经过激活函数做非线性变换，这样在多次连乘之后，前面特征对后面的影响就自然变小。

反向传播时也是如此，后面的误差信号在向前传播（连乘）的过程如下：

$$\begin{align} \frac{\partial E}{\partial W} &= \sum_{t=1}^{T}\frac{\partial E_t}{\partial W}\\ &=\sum_{k=1}^{t} \frac{\partial E_t}{\partial y_t} \frac{\partial y_t}{\partial h_t} \frac{\partial h_t}{\partial h_k} \dfrac{\partial h_k}{\partial W} \end{align}$$

而对于 $\frac{\partial h_t}{\partial h_k}$，有：

$$\frac{\partial h_t}{\partial h_k} = \prod_{j=k+1}^{t}\frac{\partial h_j}{\partial h_{j-1}} = \prod_{j=k+1}^{t}W^T \times diag [f'(j_{j-1})]$$

所以，

$$\frac{\partial E}{\partial W} = \sum_{t=1}^{T}\sum_{k=1}^{t} \frac{\partial E_t}{\partial y_t} \frac{\partial y_t}{\partial h_t} (\prod_{j=k+1}^{t}\frac{\partial h_j}{\partial h_{j-1}}) \frac{\partial h_k}{\partial W}$$

连乘部分有：

$$\parallel\frac{\partial h_j}{\partial h_{j-1}} \parallel \leq \parallel W^T\parallel \parallel diag [f'(h_{j-1})]\parallel \leq \beta_W \beta_h$$

其中 $\beta_W, \beta_h$分别是矩阵和向量的L2范式。

那么，

$$\parallel \dfrac{\partial h_t}{\partial h_k} \parallel = \parallel \prod_{j=k+1}^{t} \dfrac{\partial h_j}{\partial h_{j-1}}\parallel \leq (\beta_W \beta_h)^{t-k}$$

显然，若 $\beta_W\beta_h$显著地大于或小于1的时候，经过足够多的t-k次乘法之后就会趋近于0或者无穷大。小于1更常见，会导致很长时间之前的词语无法对当前的预测产生影响。

大于1时，浮点数运算会产生溢出，一般会很快发现，即为梯度爆炸。小于1，并不会产生异常，难以发现，只是效果会显著降低，即为梯度消失。

4. 梯度爆炸和消失的防止

梯度裁剪

这是一种暴力的方法，当梯度的长度大于某个阈值的时候，将其缩放到某个阈值。通常用于梯度出现NA的时候。

参数初始化

与其随机初始化参数矩阵，不如初始化为单位矩阵，这样初始效果就是上下文向量和词向量的平均。

改变激活函数

不采用sigmoid函数，而是relu或它的变体，结合上面的初始化方法，在很深的网络中依然可以训练。

5. 问题

这个问题是来自在语言模型的应用中，分类要用到softmax，词表太大的话，softmax会很费力，一个技巧是，先预测词语的分类（比如按词频划分），然后在分类中预测词语，分类越多，困惑度越小，但速度会更慢。

6. 应用

最后介绍了RNN序列模型在NER，机器翻译的应用。这个就不多说了，值得注意的是，rnn引申到了seq2seq，即encoder-decoder模型，在机器翻译中，encoder和decoder使用不同的权值矩阵，效果会更好，这是个小trick吧，这样会使模型有更好的泛化能力。另外，decoder的输入来自三个方面： $h_t$，前一个预测值和encoder的最后一个隐藏层。

7. 总结

RNN应用了简单的循环结构，长距离依赖问题还是无法解决，所以在实际的应用中，通常是用有更好性能的变体：LSTM或GRU，将在下节介绍。