cs224n lecture 2 note：word vectors

Published: November 04, 2018 by Learner | Hits:

• Categories:
• cs224n 8

• Tags:
• notes 8

1. 为什么要使用word embedding?

在信号处理领域，图像和音频信号的输入往往是表示成高维度、密集的向量形式，在图像和音频的应用系统中，如何对输入信息进行编码显得非常重要和关键，这将直接决定了系统的质量。在自然语言处理中也类似，传统做法是给单词标号，每个词表示为index处为1，其他位置为0，总长度为词表大小的one-hot形式，这样做有很明显的缺点，如下所示。

• 词语直接缺乏关联
• 难以存储和维护
• 难以计算词语相似度

而Word Embedding技术则可以解决上述传统方法带来的问题。

2. 对word embedding方式的探索

'You shall know a word by the company it keeps', 正如这句话所述，人们试图构造出低维稠密词向量，之后最大化$p(context\ |\ w_t)$，也就是最小化如下loss：

$$loss = 1 - p(context\ |\ w_t)$$

或者

$$loss = 1 - p(w_t\ |\ context)$$

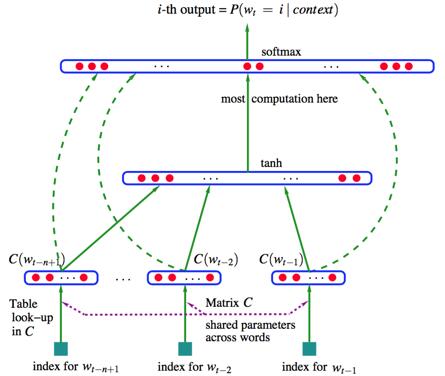
这体现了预测的思想（实际上，还有一种统计思想，将在第三节介绍），在word2vec之前，有下图所示的神经概率语言模型，我想这个模型对word2vec有很大的影响，word2vec正是基于这个模型做了精简，并针对该模型的缺点做了改进。

3. Skip-Gram

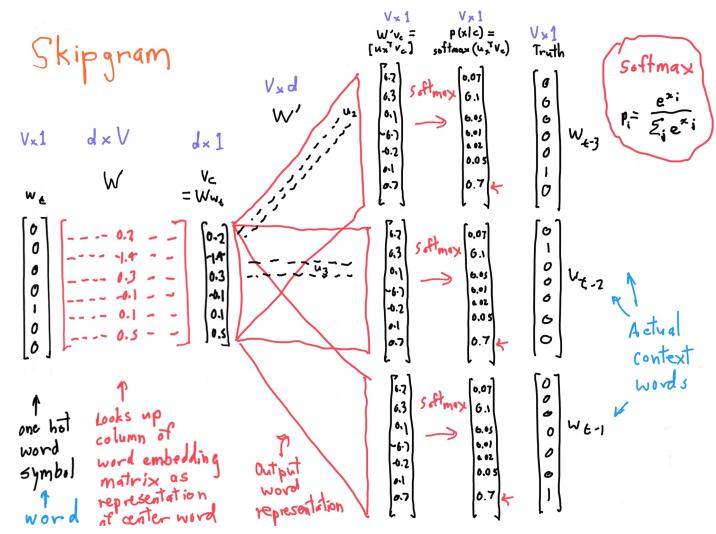
Word2vec是一个典型的预测模型，用于高效地学习word embedding。实现的模型有两种：连续词袋模型(CBOW)和Skip-Gram模型。算法上这两个模型是相似的，只不过CBOW是从输入的上下文信息来预测目标词；而Skip-Gram模型则是相反的，从目标词来预测上下文信息。一般而言，这种方式上的区别使得CBOW模型更适合应用在小规模的数据集上，能够对很多的分布式信息进行平滑处理；而Skip-Gram模型则比较适合用于大规模的数据集上。课程里是以skip-gram为例进行讲解。skip-gram的模型类似于上图，但是只有三层，分别为：输入层，隐藏层，输出层，如下图所示。

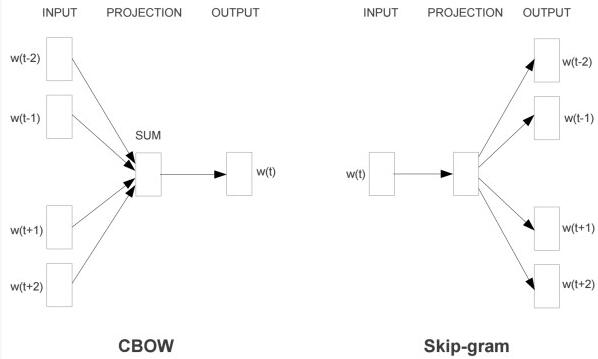
下图是skip-gram具体的例子

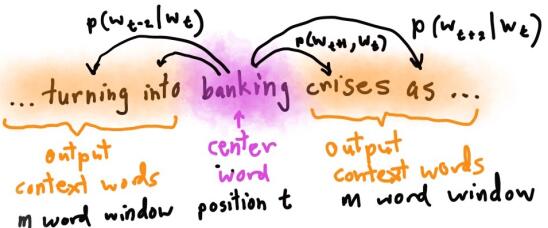
根据中间词（banking）预测window范围内的上下文(turning into…)，假设有T个词，window大小为m，当前词为$w_t$，则损失如下：

$$J(\theta)=\prod_{t=1}^T\prod_{-m \leq j \leq m \atop j \neq 0}P(w_{t+j}\ |\ w_t;\theta)$$

对应的似然损失为：

$$J(\theta)=-\frac{1}{T}\sum_{t=1}^T\sum_{-m \leq j \leq m \atop j \neq 0}\log(P(w_{t+j}\ |\ w_t))$$

可见，模型的关键是求出 $P(w_{t+j}|w_t)$ ，我们要根据center word去预测out words(context words)，可以对输出层的输出结果做softmax操作，得到一个归一化的，概率性的结果，只要让out words的概率值最大就好。这样就得出了word2vec中对 $P(w_{t+j}|w_t)$ 即 $P(o|c)$ 的定义。

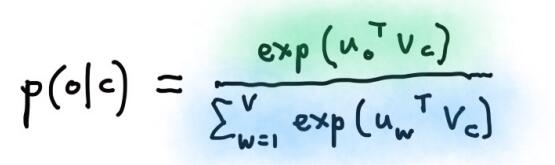
下图形象的展示了这个过程：

4. 梯度计算

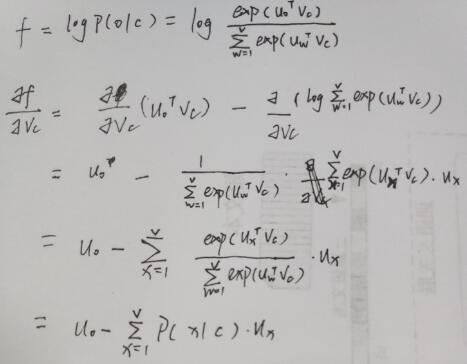
5. Trick

这节课只是简单地讲了Skip-Gram的原理，对于word2vec的一些trick并未介绍。在这里简单记录一下。

• Hierarchical Softmax

  不管是CBOW还是Skip-Gram在最后都要求softmax做归一化，分母要计算词表大小个指数运算，而层次级softmax是将复杂的归一化概率分解为一系列条件概率乘积的形式。word2vec按照词频构造哈夫曼树，也就将V个词的归一化问题转换成了log(V)个词的概率拟合问题。乘积中的每一项都是逻辑回归函数，$D_1,D_2\ldots D_n$是每个分枝的取值，左为1，右为0，表示如下：

  $$p(w_t|context)=p(D_1=1|context)p(D_2=0|D_1=1)\ldots p(w_t|D_k=1)$$

• Negative Sample

  负采样摒弃了霍夫曼树方法求解概率，而是认为当前窗口内的词是正例，那么从窗口外以某种方式采样得到的若干词是负例，就更加容易得到概率值，并且每次只需更新部分词表中的向量。而采样方式，就是按照词频的0.75次方排序，依概率采样。

• 过采样

  这是为了解决像诸如：the, a, an 等频率极高又对预测贡献不大（和很多词都可搭配）的词的影响。以如下概率删除一些高频词：

  $$P_{drop}(w)=1-\sqrt[]{\frac{t}{f(w)}}$$

  t一般取$10^{-5}$，f(w)表频率，$P_{drop} > threshold$ 即被删除，我在实现中 threshold设为0.8

  

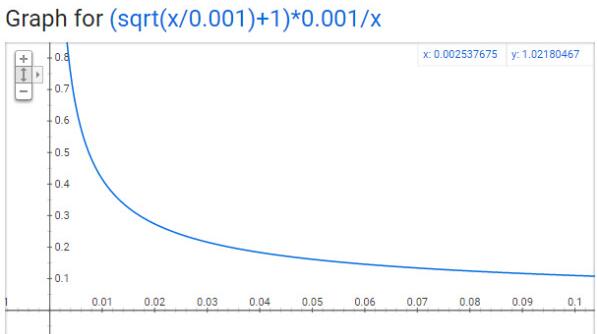
  横轴表示频率，纵轴表示被保留下来的概率。公式与上面写的略有不同，一个是论文上的公式，一个是代码实现上的公式。

6. 总结

word2vec是我研究生阶段的启蒙知识。还没入校的时候，导师发过来一份电子版的《word2vec中的数学原理》，当时看得晕头转向，入学后不同阶段多次翻出来看，虽然看的多，但其实认识并不深（只学习框架上的内容），倒是每次看都会有不同的理解。不过想象中的理解落实在博客上还是有难度，有些地方还是要查查资料，虽然写下来了难免会有理解错误的部分，是时候以数学的角度再看一次《数学原理》了。