句子单词之间解析距离的计算
最近在读aspect-level情感分类论文的时候,看到一个attention机制的改进,实现起来比较有意思,做一下记录。通常,我们在对句子做attention的时候,对句子中的每个单词都是同等看待的,attention得到的结果再作用到每个单词的隐层表示上去,作为权重。而在方面级情感分类中,针对一个特定方面,不同位置的单词显然作用是有差别的,因此就有了基于与aspect words距离的权重设计,但还是考虑了句子的所有单词,这篇论文的作者则更进一步,直接基于解析距离来做,设置距离阈值,大于该阈值的直接不考虑(即权重为0),取得了不错的效果,那么该怎么计算呢?
句子的解析以及解析距离示例如下图所示。
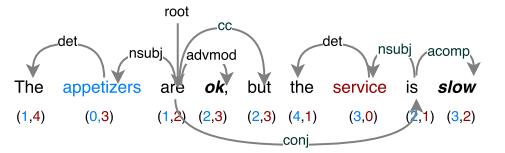
彩色为aspect word, 括号内为每个词到各个aspect间的解析距离。
从这个图可以看到是个多叉树,问题就转换成了求多叉树的某一结点与其他结点的距离,很容易想到,两个结点的距离是它们分别到最近公共结点的距离之和。而根结点是所有结点的共同祖先,根结点到其他结点的距离就是其他结点的高度值,理清楚这一点,就好做了。
一开始看着解析结构没想到是树,就没想出来怎么做,建模思想有待提高。另外,不知道是不是因为句子不规范,有个长句子有两个root,导致程序在找公共祖先的时候陷入死循环(分属不同的解析树),改正后实验效果还不错。代码如下,顺便复习了层次遍历~~
句法解析用的spaCy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def find_common_ancestor(self, asp, t):
tmp = t.head
while True:
if asp in tmp.subtree:
break
else:
tmp = tmp.head
return tmp
def get_dependency_dist(self, doc, asp_id):
root_lst = [t for t in doc if t.head == t]
weights = [self.ws+1] * len(doc) # 初始距离设置为 阈值+1 , 表示不可达
for root in root_lst: # 可能有多个root,如果不找到相关的root,
if doc[asp_id] in root.subtree: # 求最近公共祖先的时候可能会死循环
break
myDeque = deque()
myDeque.append(root)
height = 0
to_be_print = 1
next_num = 0
while len(myDeque) != 0: # 层次遍历,确定结点到根结点的距离
token = myDeque[0]
weights[token.i] = height
descendant = [x for x in token.children]
tmp_num = len(descendant)
if tmp_num != 0:
for d in descendant:
myDeque.append(d)
next_num += 1
myDeque.popleft()
to_be_print -= 1
if to_be_print == 0:
to_be_print = next_num
next_num = 0
height += 1
w_cache = weights.copy()
gap = weights[asp_id]
weights[asp_id] = 0
for idx, token in enumerate(root.subtree):
if idx == asp_id:
continue
if token in doc[asp_id].subtree: # 两结点本身就是祖孙关系
weights[idx] -= gap
elif doc[asp_id] in token.subtree:
weights[idx] = gap - weights[idx]
else: # 否则就是 各自到根结点的距离相加再减去root到公共结点距离的2倍
ans_t = self.find_common_ancestor(doc[asp_id], token)
weights[idx] = weights[idx] + gap - 2 * w_cache[ans_t.i]
return weights